Diffusion within sediment and at interface

• Diffusion into the sediment is computed resolving following equations 1 (after Consolidation Process processes or not)

  \(\frac{\partial (dzs_k*\varphi_k*Cs_k)}{\partial t}=+F_k-F_{k-1}\) (Equation 1A)

  
  

  \(F_k=\phi i_k^{t+dt}*Ds_k*\frac{Cs_{k+1}^{t+dt}-Cs_{k}^{t+dt}}{dzsi_k}-Wsi_k*(c_{ex}Cs_{k+1}^{t+dt}+f_{ex}Cs_{k}^{t+dt})\) (Equation 1B)

• with :

  • \(Cs_k^{t+dt}\) : dissolved substance concentration into layer k and at time t+dt (Mass/m^3[pw] [pw:pore water])
  • \(F_k\) : Flux at interface between layer k and layer k+1 (Mass/T/m^2[sed])
  • \(dzs_k\) : thickness of layer k (m[sed])
  • \(dzsi_k\) : intermediate thickness between Cs_k and Cs_{k+1} (m[sed])
  • \(\varphi_k^{t}\) : porosity into the layer k at time t (m^3[pw]/m^3[sed])
  • \(\phi i_k^{t}\) : intermediate porosity at the interface between the layer k and the layer k+1 at time t (m^3[pw]/m^3[sed])
  • \(Ds_k\) : Effective dispersion coefficient (m^2[sed]/T), corrected by tortuosity \(\theta\) (see Eq 1C)
  • \(Wsi_k\) : transfert rate of pore water at the interface between the layer k and the layer k+1 [m^3[pw]/m^2[sed]/T)
  • \(f_{ex},c_{ex}\) : factors upstream decentering for advection (\(f_{ex}=1\) : completely upstream evaluation)
  • \(Ds_k=\frac{D_0}{\theta^2}\) and \(\theta^2=1-\ln(\varphi^2)=1-2*ln(\varphi)\) (Boudreau,1997)

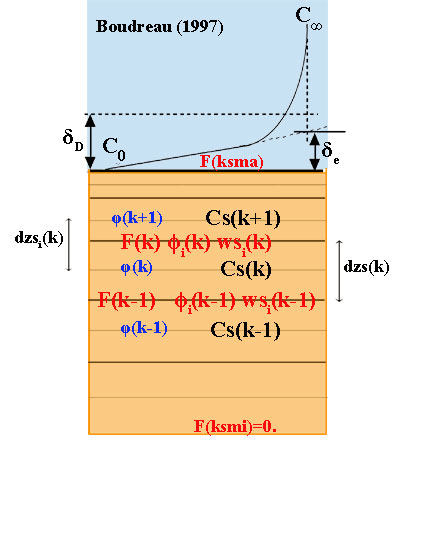
• At bottom , F(k-1)=0.

• At sediment surface (water-sediment interface) (k=ksmax) :

  • \(F_k=\beta (C_{wat}^{t+dt}-Cs_k^{t+dt}) - Wsi_k*Cs_k^{t+dt}\)

  • Three expressions are proposed here (dependent of choice_flx_diffsed given in paraMUSTANG.txt)

    • choice_flx_diffsed =1

      : Fick law with diffusive sublayer supposed to be = half the thickness of the bottom layer

      • ==>> \(\beta=2.*\frac{Ds_k}{dzsi_{ksmax}+dz(1)}\)

    • choice_flx_diffsed given =2

      : Fick law with diffusive sublayer supposed to be = distance epdifi (given in parasedim.txt)

      • ==>> \(\beta=\frac{Ds_k}{0.5*dzsi_{ksmax}+epdifi}\)

    • choice_flx_diffsed given =3

      : formulation proposed by Boudreau (1997)

      • ==>> \(\beta=\frac{Ds_k}{\delta_e}\)
      • \(\delta_e\) : thickness of an effective diffusive sublayer that has a completely linear gradient and has the same flux as the real diffusive sublayer of thickness \(\delta_e\) (see fig)
      • \(\beta=0.0889 U_* Sc^{-0.704}\) : formulation of Shaw and Hanratty (1977) in Boudreau (1997) (U_* is the shear velocity and Sc is the Schmidt number)