Parametrization and closures

Turbulence models

Three classes of turbulent closure models have been included in the MARS modelling system.

  • Numerous models based on algebraic relations exist. The following formulations are actually implemented in the MARS model code.

    • Constants coefficient

      Regarding nuV and kapaV , in the MARS modelling system we recommend a constant viscosity
      between 10e−4 (kinematic viscosity) and 10e−1 m2/s (the largest value measured in situ)

    • Prandtl’s law

      Prandtl derived the logarithmic velocity distribution near a solid surface by using a mixing length theory

    • Quetin

      based on density stratification

    • Pacanowski & Philander

  • Single equation models

    With this approach, the eddy viscosity (resp. the diffusivity) is set as a function of a turbulent velocity V and a mixing length lm
    • Turbulent Kinetic Energy
    • Mixing length

  • Two equations models

  • Horizontal diffusion

Air_sea interactions

The thermal structure of the upper ocean layer is quite complex due to the time and space variability of wind stress and heat fluxes. The heat fluxes at the sea surface, combined with the wind, induced turbulent mixing near surface layer cause temperature variations within the upper layers and consequently, density stratification.

Vertical boundary conditions

The flux at the upper and lower boundaries of the domain together with kinematic conditions leads to the following sets of equations :

  • at surface (\(\sigma=0\))

  • \(\frac{nz}{D}\frac{nz}{D}\frac{\partial u}{\partial \sigma }=\frac{\tau_{sx}}{\rho_0}\)

  • \(\frac{nz}{D}\frac{nz}{D}\frac{\partial v}{\partial \sigma }=\frac{\tau_{sy}}{\rho_0}\)

  • \(\frac{kz}{D}\frac{nz}{D}\frac{\partial T}{\partial \sigma }=\frac{Q_T}{\rho_0 C_p}\)

  • \(kz \frac{\partial S}{\partial \sigma }=0\)

  • \(w^{\stackrel{0}{a}}=0\) = vertical velocity components


  • \((\tau_{sx}\) , \(\tau_{sy})=\rho_a Cd_s \parallel \overrightarrow{W} \parallel (W_x\) , \(W_y)\)
D= height of water column, D = H + \(\xi(x,y)\)
nz=vertical eddy viscosity ; kz=vertical eddy diffusivity
u,v = zonal, meridian velocity components
\(\tau_{sx},\tau_{sy}\) = surface stress components
\(\rho_0\) = water density ; \(\rho_a\) = air density
T,S = Temperature & Salinity
Q_T = heat flux at the air_sea interface
Cd_s = surface drag coefficient
\((W_x\) , \(W_y)\) = wind velocity vector
at 10 m above the sea surface
  • at bottom (\(\sigma=-1\))
  • \(\frac{nz}{D}\frac{nz}{D}\frac{\partial u}{\partial \sigma }=\frac{\tau_{bx}}{\rho_0}\)
  • \(\frac{nz}{D}\frac{nz}{D}\frac{\partial v}{\partial \sigma }=\frac{\tau_{by}}{\rho_0}\)
  • \(\frac{kz}{D}\frac{nz}{D}\frac{\partial T}{\partial \sigma }=0\)
  • \(kz \frac{\partial S}{\partial \sigma }=0\)
  • \(w^{\stackrel{0}{a}}=0\)
  • \((\tau_{bx}\) , \(\tau_{by})=\rho_a Cd_B \parallel \overrightarrow{u} \parallel(u\) , \(v)\)
  • \(Cd_B=(\frac{\kappa}{ln{\frac{z+h+z_0}{z_0}}})^2\)
D= height of water column, D = H + \(\xi(x,y)\)
nz=vertical eddy viscosity ; kz=vertical eddy diffusivity
u,v = zonal, meridian velocity components
\(\tau_{bx},\tau_{by}\) = bottom stress components
\(\rho_0\) = water density ;
T,S = Temperature & Salinity
\(\kappa\) =Von Karman constant ; z_0 = bed roughness

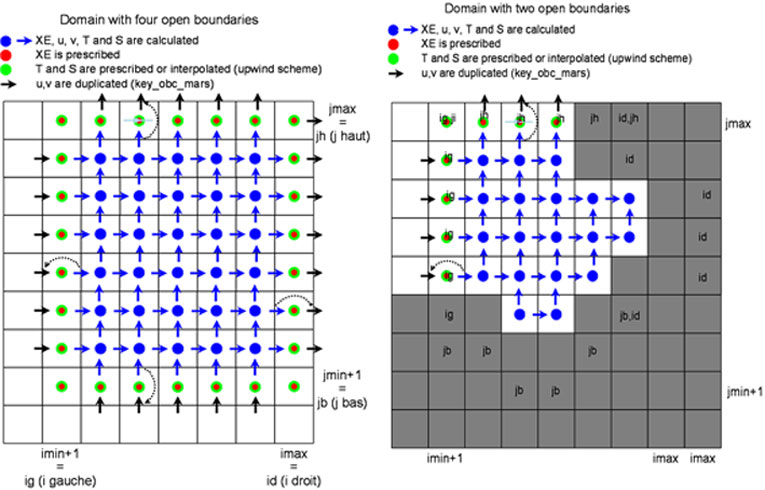
Open boundary conditions

Numerical models of finite coastal regions inevitably involve the treatment of open boundaries where the numerical grid ends. Ideal open boundaries are ”transparent” to motions which are generated within the computational domain and which are ”felt” at the open boundaries. There is no numerical treatment of open boundaries which achieves this ideal. A large number of open boundary conditions have been proposed in the past (Palma & Matano, 1998 [29]). Due to the essentially hyperbolic nature of the incompressible, hydrostatic primitive equations, external data is required for only inward boundary fluxes. The outward fluxes may be treated with an algorithm for two-dimensional radiation. In the MARS model the prescription of the Open Boundary Conditions (OBCs) is based on the method of characteristics.

_images/schema_discretisation_obc.jpg

Moving boundaries

In shallow coastal areas, some areas may dry up at low water level, which means that we have moving boundaries. The definition of these boundaries would appear to be rather straightforward : the instantaneous water depth h = 0 (h is defined by eq. (1.31)). Several techniques have been developed to track the moving boundaries. However, there are some difficulties involved in applicable numerical models.

In the MARS model, the wetting and drying processes have been cleared up by introducing a water depth H on each side of a grid cell

Forcings

  • Momentum equations
    • Winds
    • Tides
    • River discharges (mass)
  • Thermodynamics
    • Heat fluxes (LW, SH, latent, sensible)
    • River discharges (salinity, temperature)